Центральное проецирование

Центральное проецирование является наиболее общим случаем получения проекций геометрических фигур. Сущность его заключается в следующем: пусть даны плоскость α и точка S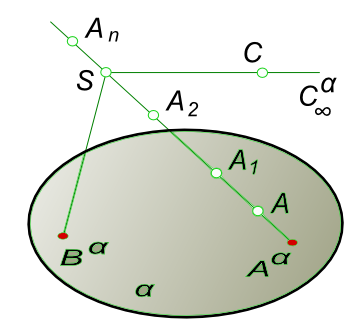

Центральное проецирование

Возьмем произвольную точку A, не принадлежащую плоскости α. Через заданные точки S, A проведем луч SA и отметим точку A^α, в которой этот луч пересекает плоскость α. Плоскость α называют плоскостью проекции, точку S- центром проекции, полученную точку A^α-центральной проекцией точки A на плоскость α, [SA^α)-проецирующим лучом. Положение плоскости α и центра S определяет аппарат центрального проецирования. Если он задан, то всегда имеется возможность определить положение центральной проекции любой точки пространства на плоскость проекции.

Действительно, пусть дана произвольная точка B, проведя через нее проецирующий луч и определив точку его встречи с плоскостью α, определяем центральную проекцию B^α точки B приданном аппарате проецирования (α и S). В том случае, когда точка C принадлежит плоскости, проходящей через центр проекции и параллельной плоскости α, проецирующий луч SC пресечет плоскость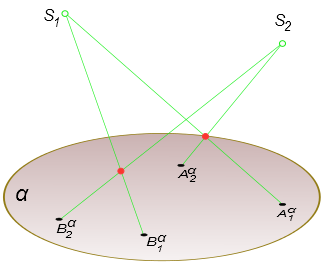

Центральное проецирование

проекции в несобственной точке C^α_∞. Так как через две различные точки можно провести одну и только одну прямую,то из рассмотрения рисунка можно сделать вывод, что при заданном аппарате проецирования - фиксированном положении точки S и плоскости α, каждая точка пространства будет иметь одну и только одну центральную проекцию. Обратное утверждение - каждой центральной проекции точки однозначно соответствует точка пространства - не имеет смысла.

Действительно кроме точки A^α на проецирующем луче кроме точки A расположено множество точек A₁, A₂, A_..., A_n. Поэтому одна центральная проекция точки не дает возможности судить о положении самой точки в пространстве.

Для того чтобы сделать возможным определение положения точки в пространстве по ее центральным проекциям, необходимо иметь две центральные проекции этой точки, полученные из двух различных центров. Имея две центральные проекции точки A^α₁ и A^α₂, полученные из центров S₁ и S₂, можно определить положение точки A в пространстве. Для этого достаточно провести проецирующие лучи и отметить точку их пересечения.

Аналогичные рассуждения можно применить к точке B.