Вращение вокруг горизонталиВращение вокруг горизонтали плоскости, дает возможность перевести ее в положение, параллельное плоскости H, и получить неискаженный вид горизонтальной проекции. Вращение плоскости вокруг фронтали позволяет перевести ее в положение, параллельное плоскости V, что обеспечит получение неискаженного вида фронтальной проекции. При таком положении плоскости ортогональная проекция любой принадлежащей ей фигуры на одну из плоскостей проекций будет конгруентной оригиналу и, следовательно, позволит определить все метрические характеристики фигуры по этой ее проекции. Когда происходит вращение вокруг горизонтали, окружность, представляющая траекторию точки, будет проецироваться на плоскость H в отрезок прямой, перпендикулярной горизонтальной проекции горизонтали. Вращение вокруг горизонтали точки A 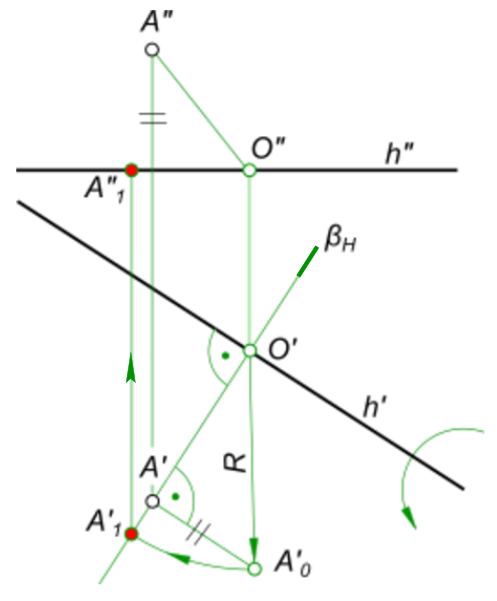 Вращение вокруг горизонтали Вращение точки вокруг фронтали плоскости α(b ∩ d) 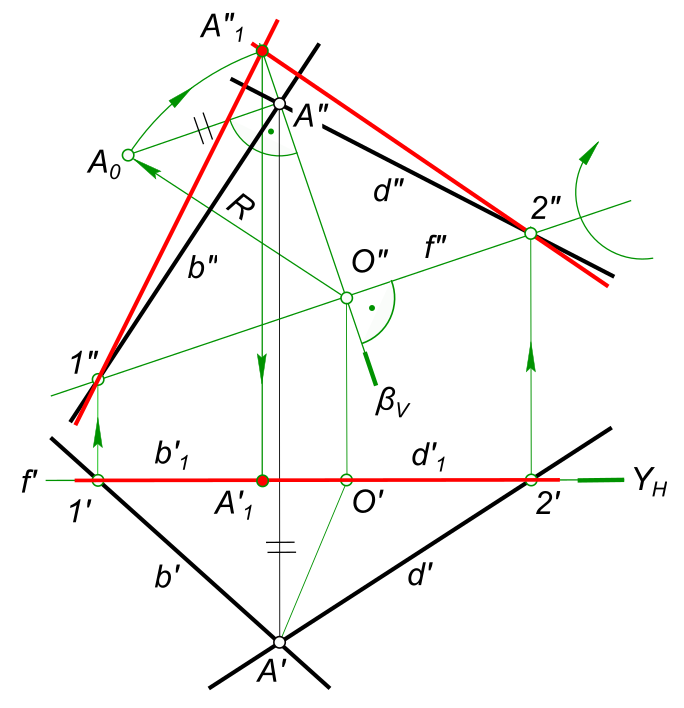 Вращение вокруг горизонтали Плоскость α, заданную пересекающимися прямыми b и d, переводим в положение параллельное плоскости V: - проводим горизонтальную проекцию f` фронтали f, по точкам 1 и 2 определяем положение фронтальной проекции f" фронтали f; - через точку A проводим фронтально проецирующую плоскость β перпендикулярную фронтали f и на их пересечении определяем центр вращения O(O" ⇒ O`); - определяем радиус вращения R, как гипотенузу прямоугольного треугольника O"A"A0; - из центра O" проводим дугу радиусом O"A0 и на ее пересечении с прямой (O"A") находим положение проекции A"1, а затем и A`1. Точка A1 совместно с прямой f (точками 1, 2) определяет плоскость α1║V. Используя вращение вокруг горизонтали 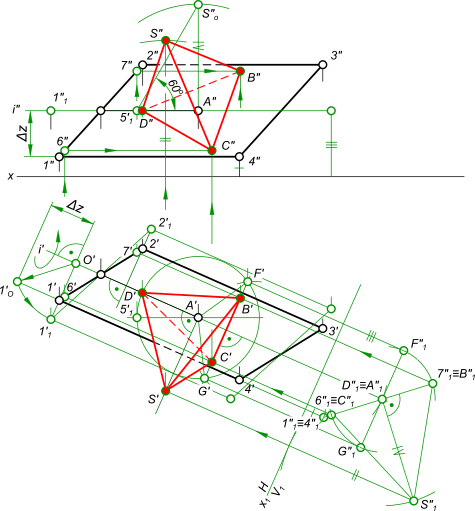 Вращение вокруг горизонтали построить правильную треугольную пирамиду с основанием в плоскости 1-2-3-4 и центром основания в точке A. Наклон боковых ребер к основанию равен 60°. Правильная треугольная пирамида имеет в основании равносторонний треугольник и одинаковые боковые грани. Плоскость основания 1-2-3-4 образована двумя парами параллельных прямых 1-3, 2-4 и 1-2, 3-4, причем стороны 1-3 и 2-4 представляют собой горизонтали так как их фронтальные проекции параллельны оси x. Центр основания в точке A, аналогично определяем расположенным на горизонтали. Плоскость основания 1-2-3-4 занимает общее положение. Составим план решения: 1. Построение в плоскости основания 1-2-3-4 равностороннего треугольника - основания пирамиды; 2. Определение высоты пирамиды построением заданного угла 60 между боковыми ребрами и основанием; 3. Построение проекций вершин пирамиды; 4. Определение видимости. План решения выполняем пошагово: 1. Переводим плоскость основания 1-2-3-4 в частное горизонтальное положение вращением вокруг горизонтали i, проходящей через точку A, находя при этом ее новое положение 11-21-31-41; 2. В плоскости основания 11-21-31-41 проводим окружность максимально возможного радиуса и через ее центр A проводим фронталь 51-A; 3. На фронтальной плоскости проекций строим боковое ребро задавая угол 60° наклона его к основанию; 4. Задав положение одной из вершин основания в точке D на оси вращения i, Находим остальные вершины основания пирамиды F и G, расположенными на равном расстоянии друг от друга на дуге окружности; 5. Построение проекций вершин основания пирамиды B и C и вершины S выполняем способом перемены плоскости проекций: а) плоскость основания пирамиды горизонтальна - D1, F1 и G1; б) плоскость основания пирамиды первоначального положения проходит через точки 1"1=4"1, D"1=A"1; в) на направлении перпендикуляра из точки A"1 откладываем высоту пирамиды и находим S"1; г) в пересечении линий проекционной связи точек S"1, перпендикуляра n` к плоскости основания находим S`1; д) в пересечении линий проекционной связи точек B"1 и C"1 c F`- G`находим точки B` и C`; е) в пересечении линий проекционной связи точек B` и C` c горизонталями проходящими через 6 и 7 находим точки B" и C"; ж) отложив от оси x по линии проекционной связи точки S отрезок II находим точки S"; з) определение видимости. Вращение вокруг горизонтали применяется для решения задачи №3 по определению натуральной величины боковой грани SAC пирамиды: Графическая работа 6. +
|
