Вращение вокруг следа

    Вращение вокруг следа - совмещение, которое применяется в тех случаях когда требуется определить истинный вид фигур, лежащих в плоскости, или построить в плоскости общего положения фигуру заданной формы и размеров.
    При совмещении за ось вращения принимается не произвольная горизонталь или фронталь плоскости, а ее горизонтальный или фронтальный след. В таком случае, в результате поворота плоскости, она совмещается с плоскостью проекции H, если вращение осуществляется вокруг горизонтального следа плоскости, либо с V при вращении вокруг ее фронтального следа.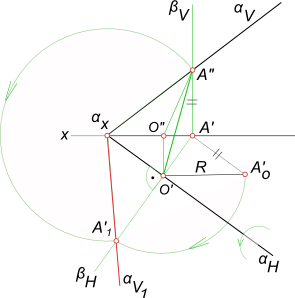

Вращение вокруг следа

    Вращение вокруг следа (сущность способа совмещения) можно уяснить из следующих рассуждений. Плоскость общего положения α (рисунок) вращается вокруг следа α_H до совпадения ее с горизонтальной плоскостью проекции. При этом преобразовании след α_H, как ось вращения, останется на месте. Поэтому для нахождения совмещенного положения плоскости достаточно найти совмещенное положение только одной, принадлежащей ей точки (не лежащей на следе α_H).

В качестве такой точки целесообразно (для упрощения геометрических построений) взять точку, принадлежащую фронтальному следу.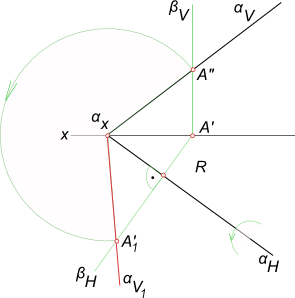

Вращение вокруг следа

Любая геометрическая фигура плоскости α, при ее совмещении с плоскостью проекции H, проецируется в конгруентную фигуру. Поэтому [a_xA"]≅[a_xA`<sub>1</sub>], указывающий расстояние от точки схода следов a<sub>x</sub> до A" на фронтальном следе конгруентен [a<sub>x</sub>A`₁] на совмещенном положении следа α_V1. В связи с этим положение точки A`<sub>1</sub>, а следовательно, и следа α<sub>V1</sub>, можно определить, не пользуясь центром и радиусом вращения. Для этого достаточно из точки a<sub>x</sub> описать дугу радиусом, равным расстоянию │a<sub>x</sub>A"│ до ее пересечения с прямой (горизонтальным следом β<sub>H</sub> плоскости β, в которой будет перемещаться точка) проведенной через A`, перпендикулярно к α_H. Через полученную точку A`₁ пройдет фронтальный след плоскости α_V1 при совмещении его с плоскостью H.

Используя вращение вокруг следа (способ совмещения) можно решить обратную задачу, связанную с построением проекций плоской фигуры заданной формы и размеров, принадлежащей плоскости общего положения

Альт

План решения задачи:
1) совмещаем плоскость, которой принадлежит фигура, с какой-либо плоскостью проекции;
2) строим на совмещенном положении плоскости требуемую фигуру;
3) "поднимаем" (поворачиваем) плоскость вместе с изображенной на ней фигурой в пространство.

Геометрические построения, которые надо выполнить, чтобы "поднять" плоскость в пространство, аналогичны построениям, выполняемым при совмещении плоскости с плоскостью проекции, только выполняются в обратной последовательности.

Найти натуральную величину треугольника ABC, принадлежащего плоскости общего положения P, способом совмещения,

Вращение вокруг следа

вращая плоскость вокруг фронтального следа.

Вращение вокруг следа используется в графической работе №12 для нахождения натуральной величины сечения пирамиды.