Проекции треугольника

Проекции треугольника,одного и того же, представлены в трех вариантах: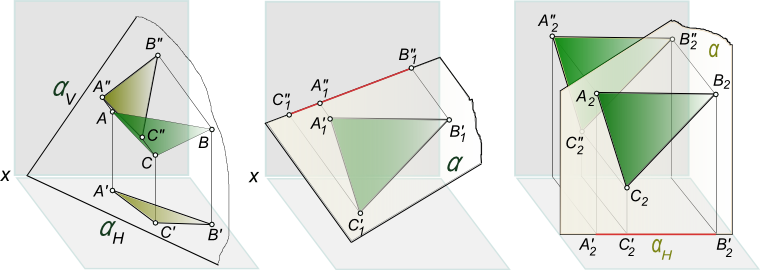

Проекции прямоугольного треугольника

1. вариант - ΔABC, занимает общее положение;
2. вариант - ΔA₁B₁C₁ ⊥ V, занимает положение перпендикулярное к фронталной плоскости проекций;
2. вариант - ΔA₂B₂C₂ ║ V, занимает положение параллельное относительно фронталной плоскости проекций;
ΔABC≅ΔA₁B₁C₁≅ΔA₂B₂C₂

Данные проекции треугольника показывают, что вид проекции (ее форма и размеры) определяются не только формой и размерами проецируемой фигуры, но и в значительной степени зависит от взаимного расположения объекта проецирования и плоскости проекций.

Действительно, три конгруентных прямоугольных треугольника ΔABC≅ΔA₁B₁C₁≅ΔA₂B₂C₂ (рисунок) в зависимости от взаимного расположения плоскости треугольника и плоскости проекции V могут проецироваться на эту плоскость в виде:
а) ΔA"B"C" соответствует ΔABC, плоскость треугольника занимает произвольное положение относительно плоскости V.
    ΔA"B"C" в метрическом отношении не имеет ничего общего с оригиналом - ΔABC (рисунок слева);
б) отрезка прямой [C"₁B"₁], в случае, когда плоскость ΔA₁B₁C₁⊥V (рисунок в центре) перпендикулярна к фронталной плоскости проекций;
в) либо в виде ΔA"₂B"₂C"₂ ≅ ΔA₂B₂C₂, когда плоскость ΔA₂B₂C₂ ║ V (рисунок справа) параллельна относительно фронталной плоскости проекций.

Сопоставляя между собой оригинал - треугольник ABC и проекции треугольника в различных положениях, мы видим, что только в случае параллельности проецируемой фигуры плоскости проекции возможно получить проекцию на эту плоскость, конгруентную самой фигуре, и, следовательно, полностью сохраняющую ее метрику.
Форма и размеры фронтальной проекции ΔA"₂B"₂C"₂ (рисунок справа) позволяют, без каких либо построений, ответить на вопросы: какова длина сторон треугольника, величина углов при вершинах, чему равна его площадь и другие метрические характеристики ΔA₂B₂C₂.

Решение задачи по определению натуральной величины треугольника ΔABC показано в статьях:
Графическая работа 3;
Натуральная величина треугольника.