Сложные перемещения

Сложные перемещения -это сочетание метода плоскопараллельного перемещения с методом перемены плоскостей проекций.

Пользуясь только одним методом плоскопараллельного перемещения или только одним методом перемены плоскостей проекций, всегда можно перейти от произвольного положения геометрической фигуры к частному, обеспечивающему получение удобного вида проекций.
Существенным преимуществом метода перемены плоскостей проекций является построение только одной вспомогательной проекции (при замене одной плоскости проекции), в то время как метод плоскопараллельного перемещения требует построения двух вспомогательных проекций (при перемещении параллельно одной плоскости).
Сочетание метода плоскопараллельного перемещения с методом перемены плоскостей проекций дает возможность использовать преимущества обеих методов.

Сложные перемещения - Первый вид состоит в том, что построение новых проекций достигается путем последовательного применения сперва метода перемены плоскостей проекций, затем способа вращения вокруг оси, перпендикулярной к плоскости проекции.
Точку A повернуть вокруг фронтали f против часовой стрелки на угол φ.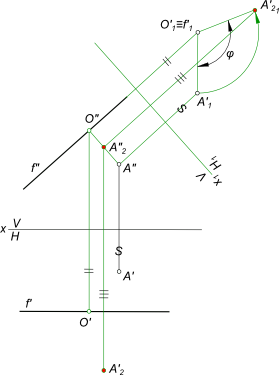

Сложные перемещения

Используем сложные перемещения для решения задачи:
- переменой одной из плоскостей проекций H преобразуем фронталь f в горизонтально проецирующую прямую f", f`₁;
- используя способ вращения вокруг оси, перпендикулярной плоскости проекции, поворачиваем точку A`<sub>1</sub> вокруг оси на заданный угол φ в положение A`2₁;
- обратным проецированием находим положение точки A2 на исходных проекциях A`₂, A"₂.

Сложные перемещения - Второй вид состоит в перемене плоскости проекции с последующим совмещением новой плоскости с той из первоначальных плоскостей, которую она заменила.

Определить высоту четырехгранной пирамиды SABC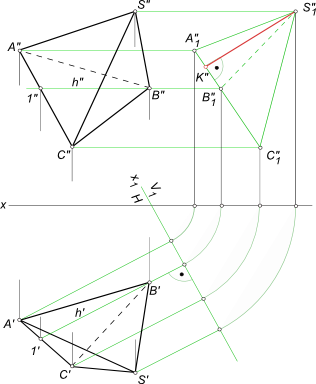

Сложные перемещения

Для решения задачи используем замену плоскости проекции V на V₁ с последующим совмещением ее с плоскостью V. Чтобы определить направление новой оси x₁, в плоскости основания ABC проводим горизонталь h (ось x₁⊥h`). Совмещаем новую плоскость V₁ с плоскостью V и строим на ней совмещенную проекцию пирамиды S"₁A"₁B"₁C"₁.

Отрезок перпендикуляра S"₁K"₁, опущенного из вершины пирамиды S"₁ на основание A"₁B"₁C"₁ определит высоту пирамиды.

Для получения ответа с помощью сочетания двух методов потребовалось построить только одну вспомогательную проекцию. Решая способом вращения, пришлось бы строить две вспомогательные проекции.