Винтовая поверхность

Винтовая поверхность может быть образована прямой линией или ее отрезком, окружностью или ее дугой, сферической поверхностью, какой либо кривой и т. п.

Винтовая поверхность, образованная винтовым движением прямой линии, относится к поверхностям, называемым линейчатыми геликоидами. Среди них различают прямой геликоид (винтовой коноид), наклонный или архимедов геликоид, эвольвентный и конволютный геликоид. Все они широко применяются в технике. Так прямой и наклонный геликоиды применяются при конструировании ходовых винтов станков, ручных прессов, домкратов и т. п., имеющих витки прямоугольного или соответственно трапецеидального профиля. Геликоиды эвольвентный и конволютный применяются при конструировании червяков, шнеков и т. п. Геликоиды применяются также при образовании поверхностей цилиндрических пружин, рессор, змеивиков, винтовых канавок в сверлах и т. п.

Винтовая поверхность имеет применение в резьбовых изделиях.
Прямая винтовая поверхность или прямой геликоид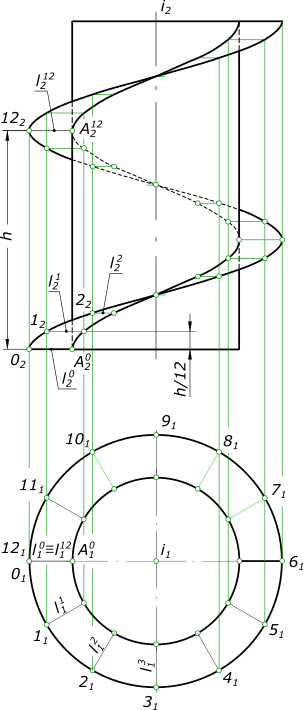

Винтовая поверхность

образуется при вращении производящей прямой линии ι, которая пересекает ось i геликоида под прямым углом, вокруг этой оси и одновременном перемещении вдоль нее на расстояние пропорциональное углу поворота
Производящая прямая ι последовательно занимает 12 положений ι0, ι1, ι2, ..., ι12. Пpи одном повороте вокруг оси и эта прямая переместится вдоль нее на расстояние равное шагу h, т. е. на величину расстояния между точками 0 и 12. Производящая прямая при своем перемещении образует геликоидную поверхность, ограниченную двумя соосными винтовыми линиями - направляющими геликоида.
Наклонная винтовая поверхность или наклонный геликоид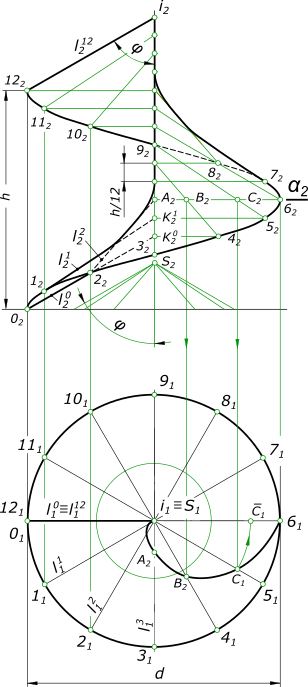

Винтовая поверхность

образуется при вращении вокруг этой оси и одновременном перемещении вдоль нее на расстояние, пропорциональное углу поворота производящей прямой линии ι, пересекающей ось i винтовой линии под некоторым углом φ.
Производящая прямая ι геликоида, пересекая при своем движении ось i прямого кругового цилиндра и винтовую линию на этом цилиндре, остается параллельной образующей некоторого прямого кругового конуса, соосного с винтовой линией.
Данными для построения наклонного геликоида служат: - цилиндр диаметра d;
- производящая прямая ι, пересекающая ось i под углом φ;
- шаг винтовой линии h.
Строим направляющий конус с вершиной S (S1, S2) и его образующие, составляющие с осью i угол φ и делящие его основание на 12 равных частей. Затем делим на то же число частей окружность диаметра d и шаг винтовой линии h.
Через точки деления фронтальной проекции i2 оси i - точки к02, к12 и т. д. проводим параллельно соответствующим фронтальным проекциям образующих направляющего конуса фронтальные проекции производящей прямой ι, т. е.: ι02=О2К02; ι12=ι2К12 и т. д.
Производящая прямая, переходя в новое последовательное положение, перемещается вдоль оси i на величину h/12 и совершает поворот на угол, равный 2π/12.
Совершая таким образом полный оборот, производящая прямая переместится вдоль оси на величину равную шагу h, займет положение ι₁12, ι₂12, описав при этом винтовую поверхность наклонного геликоида.
Очертание геликоида на фронтальной плоскости проекций представляет собой огибающую кривую ряда последовательных положений производящей прямой.
Поверхность наклонного геликоида пересекается плоскостью, перпендикулярной к его оси, по спирали Архимеда.
Плоскость α2 пересекает, показанные на чертеже положения производящей прямой в точках: A(A2), B(B2), C(C2) и 6(6₂). Горизонтальные проекции этих точек A(A1), B(B1), C(C1) и 6(6₁) по линиям связи. Для нахождения проекции A1 точки А нужно отложить на горизонтальной проекции производящей прямой ι13 от оси i1 одну четвертую ее часть, равную C16₁. Найденные точки A1, B1, C1 и 6₁ соединяем плавной кривой.