Пересечение прямой с конусом

Пересечение прямой с конусом - это задача по определению точек встречи прямой с поверхностью конуса.
Поверхность конуса состоит:
- боковой поверхности представляющей собой поверхность вращения;
- поверхности основания представляющей собой окружность .

Пересечение прямой с конусом: d ∩ α.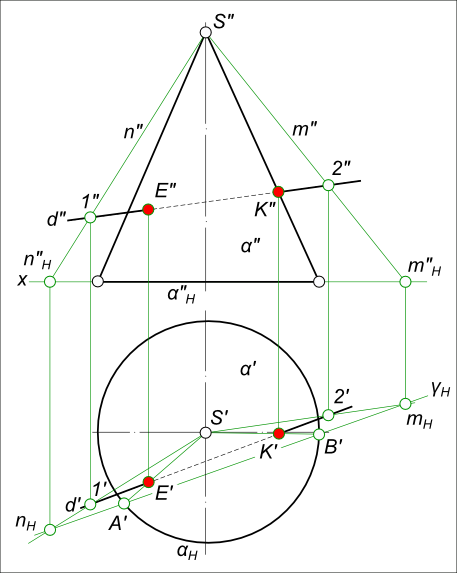

Пересечение прямой с конусом

Здесь прямая d занимают общее положение и поверхность прямого кругового конуса α формируется прямыми из вершины S. Решать задачу на пересечение прямой с конусом следует, применяя алгоритм пересечения прямой с поверхностью:
- Заключаем прямую d в вспомогательную плоскость γ, которая также проходит через вершину конуса S;
- Находим точки пересечения этой плоскости с основанием конуса, для чего строим горизонтальный след плоскости - γ_H по следам прямых n_H и m_H:
γ_H ∩ α_H = A`, B`.
Соединив полученные точки с вершиной конуса S` прямыми линиями, находим линии пересечения этой плоскости с боковой поверхностью конуса S`A`, S`B`, которые пересекаются с прямой d:
- S`A` ∩ d` = E` ⇒ E";
- S`B` ∩ d` = K` ⇒ K".

Пересечение прямой с конусом - это задача по определению видимости:
- для горизонтальной плоскости проекций производим с помощью конкурирующих точек:
- перемещаясь вверх по линиям связи точек пересечения α_H и прямой d` находим, что соответствующие точки прямой d" находится выше основания конуса α"<sub>H</sub>, а это означает что соответствующие им точки прямой d` на горизонтальной плоскости проекций видимы.
- для фронтальной плоскости проекций производим исходя из того, что образующие находящиеся:
- за очерковыми образующими не видимы;
- перед очерковыми образующими видимы.
Образующие S`A` и S`B` находятся перед очерковыми образующими и следовательно они видимы.