Пересечение прямой с пирамидой

Пересечение прямой с пирамидой - это задача по определению точек встречи прямой с поверхностью пирамиды.
Поверхность пирамиды состоит из плоских граней:
- треугольников для боковой поверхности;
- многоугольника для поверхности основания.

Пересечение прямой с пирамидой: d ∩ SABC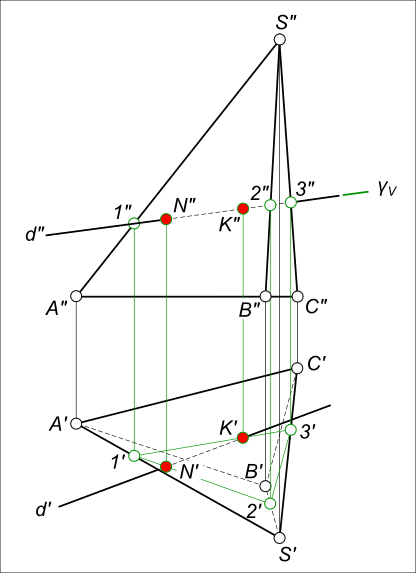

Пересечение прямой с пирамидой

Прямая d и пирамида SABC занимают общее положение, поэтому решать задачу на пересечение прямой с пирамидой следует, применяя алгоритм пересечения прямой с плоскостью:
- Заключаем прямую d в вспомогательную фронтально-проецирующую плоскость γ;
- Находим точки пересечения этой плоскости с боковыми ребрами пирамиды A, B, C:
- γ_V ∩ ребро S"A" = 1" ⇒ 1`;
- γ_V ∩ ребро S"B" = 2" ⇒ 2`;
- γ_V ∩ ребро S"C" = 3" ⇒ 3`;
- Соединив полученные точки прямыми линиями, находим их точки пересечения с прямой d и в то же время с гранями пирамиды:
- 1`-2` ∩ d` = N` ⇒ N";
- 1`-3` ∩ d` = K` ⇒ K".

Пересечение прямой с пирамидой - это также задача по определению видимости:
- для фронтальной плоскости проекций производим с помощью конкурирующих точек:
- в точке 1" имеет место пересечение ребра S"A" и прямой d", перемещаясь вниз по линии связи точки 1 находим, что соответствующая ей точка прямой d` находится ниже соответствующей ей точка ребра S`A`, а это означает что на фронтальной плоскости проекций видима точка принадлежащая прямой d";
- в точке 3" имеет место пересечение ребра S"C" и прямой d", перемещаясь вниз по линии связи точки 2 находим, что соответствующая ей точка ребра S`C` находится ниже соответствующей ей точки прямой d`, а это означает что на фронтальной плоскости проекций видима точка принадлежащая ребру S"C".
- для горизонтальной плоскости проекций определению видимости производим аналогично.