Пересечение прямой с поверхностью тора

Пересечение прямой с поверхностью тора - это задача по определению точек встречи прямой с поверхностью тора.
Поверхность тора представляет собой поверхность вращения с образующей в виде окружности.

Пересечение прямой с поверхностью тора: b ∩ α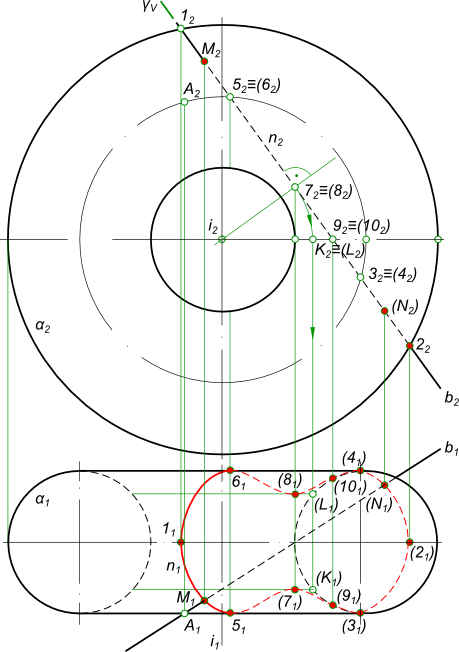

Пересечение прямой с поверхностью тора

Прямая b занимают общее положение, а тор α - фронтальное положение. Решать задачу на пересечение прямой с поверхностью тора следует, применяя алгоритм пересечения прямой с поверхностью:
- Заключаем прямую b в вспомогательную фронтально-проецирующую плоскость γ;
- Находим линию пересечения этой плоскости с поверхностью тора:
γ_V ∩ α` = n`.
Линия n в действительности представляет собой замкнутую кривую, построенную по достаточному количеству точек: 1, 2, 3 и 4, 5 и 6, 7 и 8, 9 и 10. Находим точки пересечения b₁ и n₁:
- b₁ ∩ n₁ = M₁ ⇒ M₁ ⇒ M₂;
- b₁ ∩ n₁ = N₁ ⇒ N₁ ⇒ N₂.

Пересечение прямой с поверхностью тора - это также задача по определению видимости с помощью конкурирующих точек:
- для горизонтальной плоскости проекций. Перемещаясь вверх по линиям связи точки A₁ пересечения очерковой образующей α₁ и прямой b₁ находим, что соответствующая точка прямой b₂ находится выше соответствующей точки A₂ очерковой образующей, а это означает что соответствующая им точка прямой b₁ на горизонтальной плоскости проекций видима;
- для фронтальной плоскости проекций. Перемещаясь вниз по линиям связи точки 1 пересечения очерковой образующей α₂ и прямой b₂ находим, что соответствующая точка прямой b₁ находится дальше от фронтальной плоскости проекций соответствующей точки 1₁ очерковой образующей, а это означает что соответствующая точка прямой b₁ на фронтальной плоскости проекций видима.
Перемещаясь вниз по линиям связи точки 2 пересечения очерковой образующей α₂ и прямой b₂ находим, что соответствующая точка прямой b₁ находится ближе к фронтальной плоскости проекций соответствующей точки 2₁ очерковой образующей, а это означает что соответствующая точка прямой b₁ на фронтальной плоскости проекций не видима.