Пересечение прямой с поверхностью цилиндра

Пересечение прямой с поверхностью цилиндра - это задача по определению точек встречи прямой с поверхностью цилиндра.
Поверхность цилиндра представляет собой поверхность вращения с образующей в виде прямой линии.

Пересечение прямой с поверхностью цилиндра: d ∩ α = ?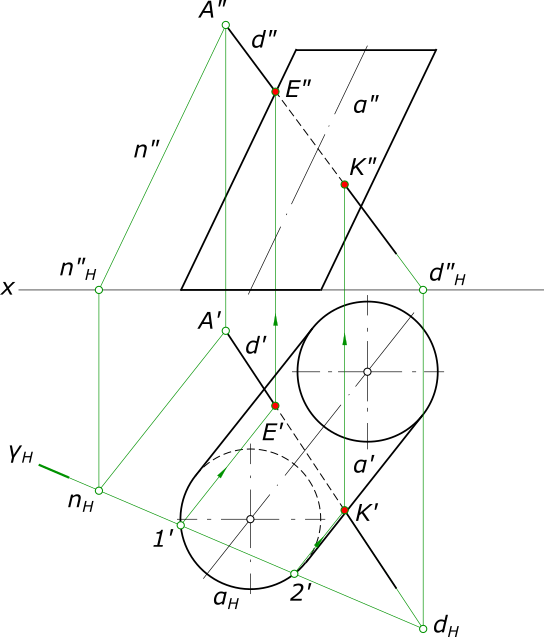

Пересечение прямой с поверхностью цилиндра

Здесь прямая d занимают общее положение и поверхность цилиндра α формируется прямыми из вершины S, находящейся в несобственной точке.
Решать задачу на пересечение прямой с конусом следует, применяя алгоритм пересечения прямой с поверхностью:
- Заключаем прямую d в вспомогательную плоскость γ, которая пересечет цилиндр по прямым линиям - образующим.
Плоскость γ задаем пересечением прямой d и прямой n параллельной образующим цилиндра;
- Находим точки пересечения 1 и 2 этой плоскости с основанием цилиндра, для чего строим горизонтальный след плоскости - γH по следам прямых nH и dH;
- В пересечении образующих цилиндра 1 и 2 с прямой d находим искомые точки E и K пересечения прямой с поверхностью цилиндра.

Пересечение прямой с поверхностью цилиндра - это также задача по определению видимости с помощью конкурирующих точек:
- для горизонтальной плоскости проекций.
Образующие 1 и 2 видимы. Прямая d видима за пределами отрезка EK;
- для фронтальной плоскости проекций.
Образующие 1 и 2 видимы. Прямая d видима за пределами отрезка EK.