Сечение пирамиды плоскостью

Сечение пирамиды плоскостью представляет собой плоскую фигуру и содержит в себе точки принадлежащие как поверхности пирамиды так и секущей плоскости.

Пирамида это многогранник - геометрическое тело боковой поверхностью которого служат плоские грани в виде треугольников. Линии пересечения граней (плоскостей) называются ребрами. В основании пирамиды находится плоский многоугольник число сторон которого соответствует количеству боковых граней. По количеству боковых граней пирамиду называют трех-, четырех-, пяти-, шестигранной и т. д.

Проекциями сечения многогранников плоскостью, в общем случае, являются многоугольники, вершины которых принадлежат ребрам, а стороны граням многогранника.

Найти сечение пирамиды плоскостью означает построение линии пересечения поверхности пирамиды (многогранника) плоскостью и сводится к многократному определению:
- либо, линии пересечения двух плоскостей (граней пирамиды и секущей плоскости), которые соединяясь между собой образуют искомую линию сечения;
- либо, точки встречи прямой (ребер пирамиды) с секущей плоскостью, которые соединяясь между собой прямыми линиями, образуют искомую линию сечения.

Построить сечение пирамиды плоскостью будет значительно проще если секущая плоскость занимает проецирующее положение.
Найти трехгранной пирамиды плоскостью a ⊥ H - горизонтальной плоскости проекций.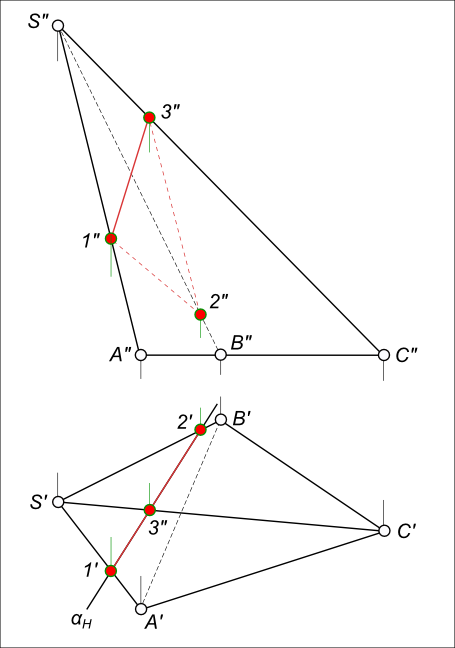

Сечение пирамиды плоскостью

На горизонтальной плоскости проекций находим точки пересечения α_H с ребрами пирамиды: 1`, 2`, 3`. На фронтальной плоскости проекций находим точки: 1", 2", 3", на пересечении линий проекционной связи с ребрами пирамиды: [S"A"], [S"B"], [S"C" ] соответственно.
Плоская фигура 1 2 3 - треугольник, есть искомое сечение пирамиды плоскостью α_H.

Построить сечение пирамиды плоскостью. Даны проекции пятигранной пирамиды SABCDE и секущая плоскость α(α_H, α_V), заданная следами.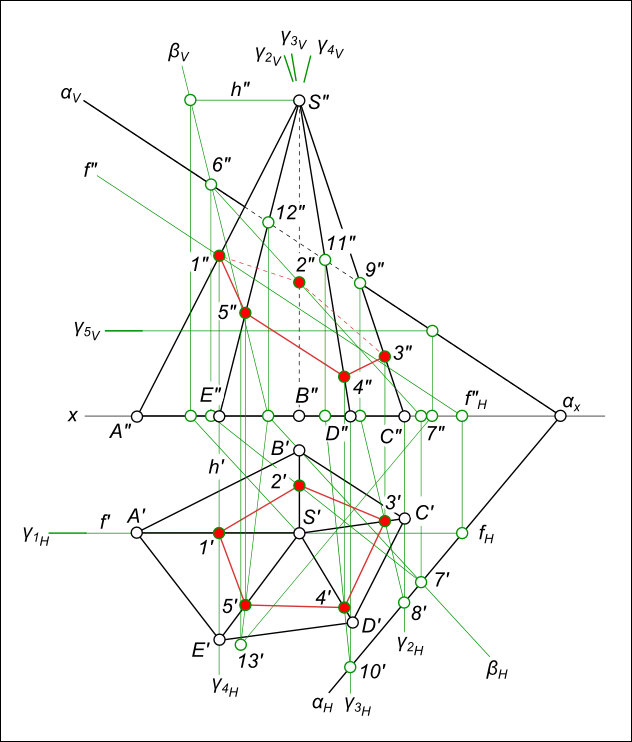

Сечение пирамиды плоскостью

Даны проекции пятигранной пирамида SABCDE и секущая плоскость α заданная проекциями трех точек 1(..., 1"), 3(3`, ...) и 5(..., 5"), принадлежащих ребрам SA, SC и SE соответственно.
Достроить линию сечения пирамиды плоскостью α.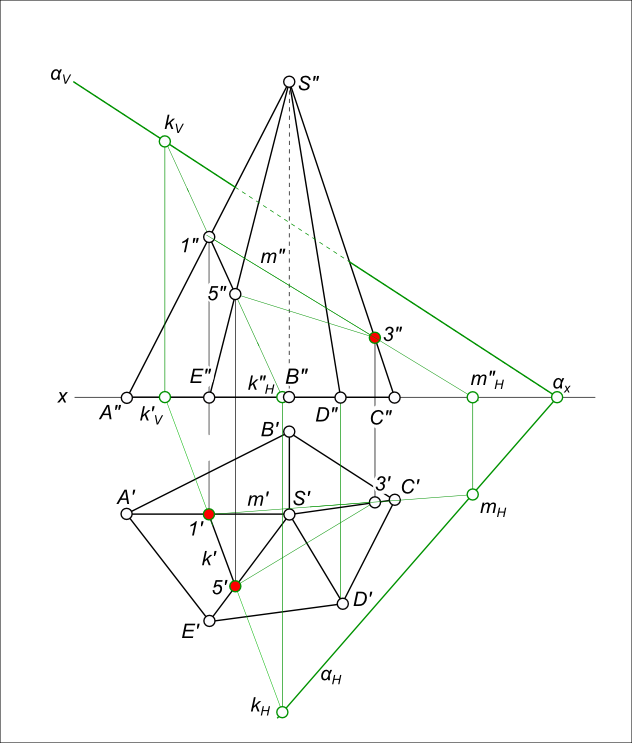

Сечение пирамиды плоскостью

если известны проекции точек лежащих на ребрах пирамиды: 1(..., 1"), 3(3`, ...) 5(..., 5").
Составляем план решения задачи:
- строим недостающие проекции для заданных точек;
- соединяем точки сечения пирамиды прямыми линиями и построив следы этих прямых линий переходим к заданию секущей плоскости α следами αH и αV.
Дальнейший ход решения задачи на сечение пирамиды плоскостью изложен в предыдущем примере.

Даны проекции пятигранной пирамида SABCDE и секущая плоскость α заданная проекциями трех точек 7(7`, 7"), 8(8`, 8"), 9(9`, 9") и 10(10`, 10"), являющихся вершинами ромба.
Построить линию сечения пирамиды SABCDE плоскостью α и его натуральную величину, используя способ перемены плоскостей проекций .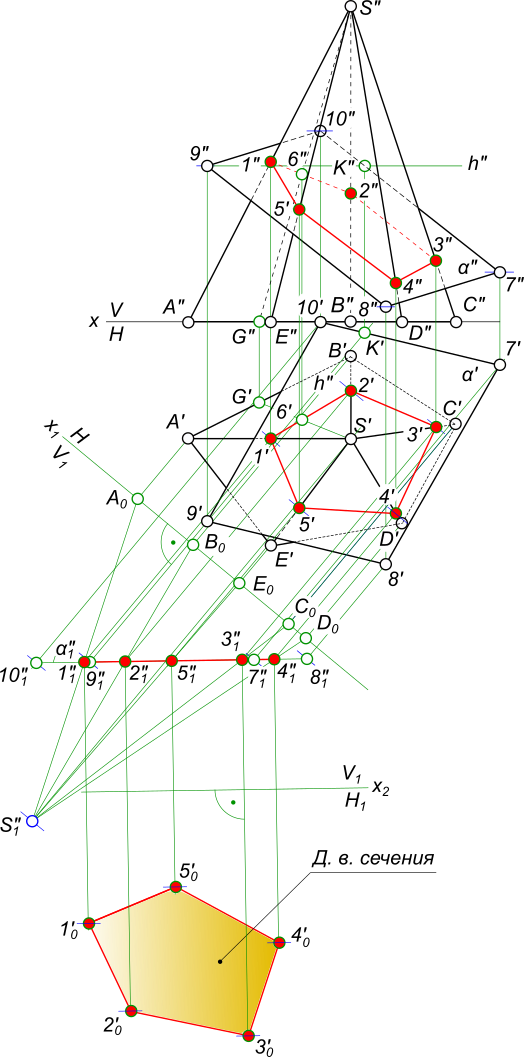

Сечение пирамиды плоскостью

Составляем план решения задачи:
Преобразуем секущую плоскость α в фронтально проецирующую:
- строится в секущей плоскости горизонталь h;
- производится Перемена плоскости проекции V на V1;
- строятся проекции секущей плоскости α"₁ и пирамиды S"₁A"₁B"₁C"₁D"₁E"₁;
- отмечаются точки пересечения ребер пирамиды с α"₁: 1"₁, 2"₁, 3"₁, 4"₁ и 5"₁;
Преобразуем секущую плоскость α(α`, α"₁) в фронтально проецирующую плоскость уровня α"₁:
- производится Перемена плоскости проекции H на H1 при этом x₂ ‖ α"₁;
- строятся точки сечения 1`<sub>0</sub>, 2`₀, 3`<sub>0</sub>, 4`₀ и 5`₀, найденные точки соединяем прямыми линиями и получаем искомую натуральную величину сечения пирамиды

Сечение пирамиды плоскостью, построенное здесь применено в статьях:
- развертка поверхности усеченной пирамиды: Развертка поверхности усеченной пирамиды;
- построение аксонометрических проекций усеченной пирамиды: Прямоугольная изометрия усеченной пирамиды;
- графическая работа 12: Графическая работа 12.