Развертка тора

Развертка тора - это приближенное решение задачи по совмещению поверхности тора с плоскостью. Потому что поверхность тора относится к неразвертываемым поверхностям.
Если заданы ортогональные проекции поверхности тора развертка тора может быть выполнена способом вспомогательных цилиндрических поверхностей.
Согласно этому способу:
поверхность тора α делят на какое-либо количество равных частей (в данном случае 12 α1, α2, ..., α12) горизонтально- проецирующими плоскостями γ1, γ2, ...,γ11, проходящими через центр тора. каждая из них подвергается апроксимации (замене) вспомогательной цилиндрической поверхностью β1, β2, ..., β12, которые строятся касательно поверхности тора.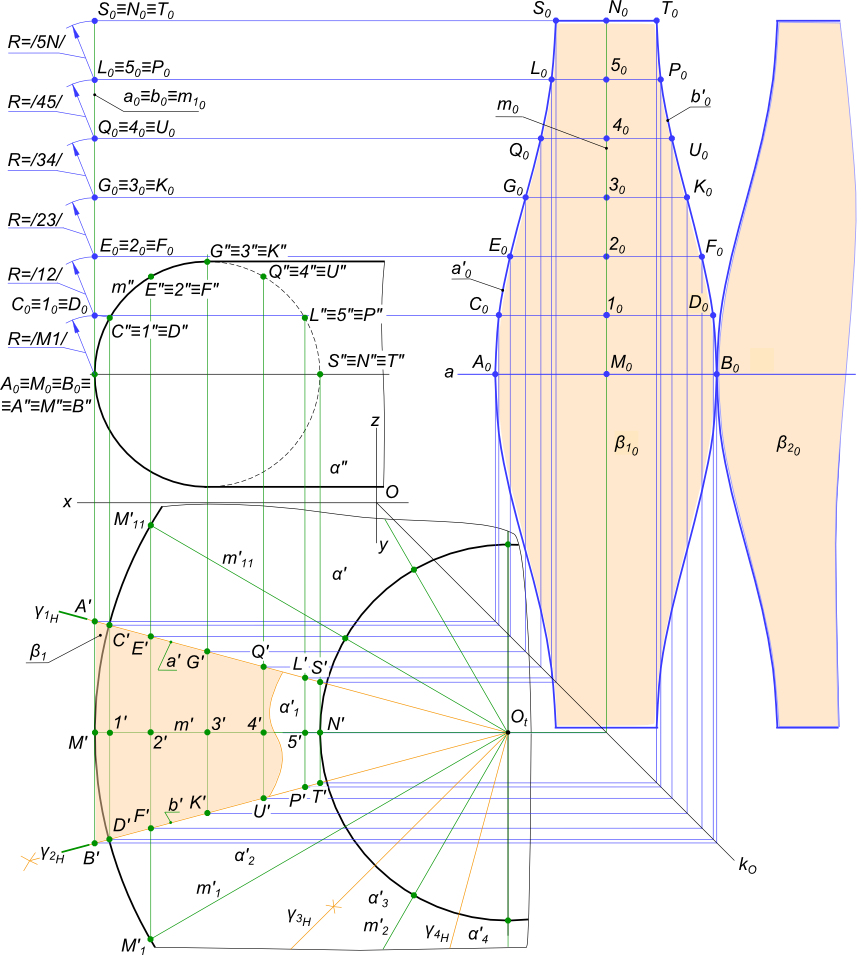

Развертка тора

развертка тора - выполняется на примере (1/12) ее части, как развертка вспомогательной цилиндрической поверхности β1:
- чтобы разделить тор на равные части выполняем деление очерковой окружности α` с помощью циркуля, отмечая точки M`, M`1, ..., M`11 и меридианы m`1, m`2, ..., m`11, проходящие через них;
- две смежных дуги очерковой окружности α` с помощью циркуля делим пополам и проводим γ1H, γ2H;
- делим дугу меридиана m" на двенадцать равных части отмечая точки M", 1", 2", 3", 4", 5", N";
- на горизонтальной проекции строим образующие цилиндрической поверхности β1 проходящие через отмеченные точки M`, 1`, 2`, 3`, 4`, 5`, N` и ограниченные секущими плоскостями в точках A` B`, C` D`, G` K`, Q`U`, L`P`, S`T` соответственно;
- на фронтальной плоскости проекций выполняем развертку меридиана m".
Подготовительные построения закончены, приступаем к построению развертки цилиндрической поверхности β1:
- проводим горизонтальную прямую a проходящую через центр тора;
- в прямоугольной системе координат строим постоянной прямую kO;
- по линиям связи строим точки развертки и соединив их плавными линиями получаем фигуру A0 S0 T0 B0, которая представляет собой приближенную развертку половины поверхности тора α1;
- пристроив к ней вторую половину симметрично относительно линии a получим развертку β10 соответствующего полной поверхности α1;
- вся развертка тора α может быть получена пристраиванием к β10, одной за другой, 11 фигур конгруентных β10.