Способ триангуляции

Способ триангуляции или способ вспомогательных треугольников применяют для построения приближенной развертки неразвертываемых поверхностей.

Дан цилиндроид α, сопрягающий две трубы одна круглого сечения другая эллиптического, причем диаметр круглой равен диаметру большой оси эллипса.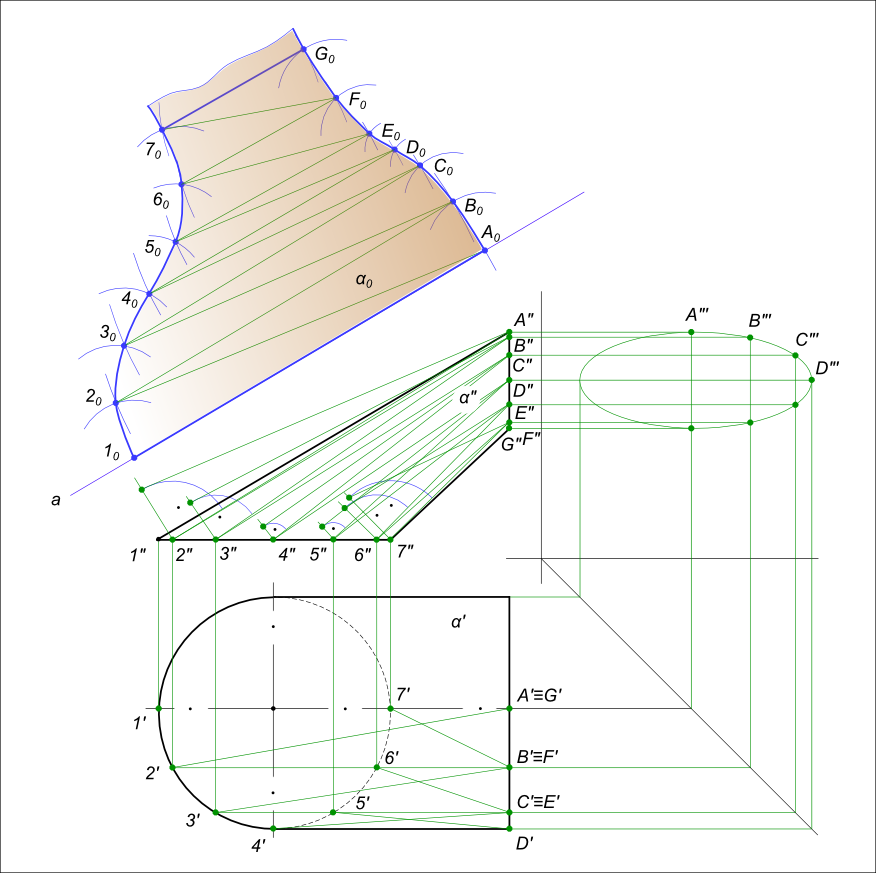

Способ триангуляции

У цилиндроида поверхность неразвертываемая. Поэтому применяем способ триангуляции - аппроксимируем ее вписанной многогранной поверхностью состоящей из треугольников. На поверхности цилиндроида проводим ряд прямолинейных образующих, параллельных плоскости параллелизма:
- 1A, 2B, 3C, 4D, 5E, 6F и 7G.
Здесь плоскостью параллелизма выступает фронтальная плоскость проекции.
Участок поверхности между смежными образующими 1A и 2B разделим диагонально 2A на два участка, которые считаем треугольниками. Таким же образом разделим на элементарные треугольники все остальные участки находящиеся между образующими.

Выполняем построение развертки многогранной поверхности состоящей из элементарных треугольников:
- проводим на свободном месте чертежа произвольную прямую a;
- откладываем на ней первую образующую [1₀A₀] ≅ [1"A"];
- проводим дуги радиусом [1`2`] и радиусом |A`2`|, на их пересечении находим точку 2₀. Натуральную величину [A2] определяем способом прямоугольного треугольника;
- соединяем точки A₀ и 2₀ прямой линией;
- из точки 2₀ строим вторую образующую [2₀B₀] ≅ [2"B"];
- проводим дуги радиусом [2"B"] и радиусом [A"`B"`],на их пересечении находим точку B₀;
- соединяем точки 2₀ и B₀ прямой линией.
Аналогично строим другие точки развертки, которые соединяем плавной кривой. На рисунке показано построение половины развертки потому, что вторая половина ей симметрична.

Способ триангуляции применяют для построения развертки поверхности пирамиды: Способ треугольников.

Способ триангуляции или способ треугольников использован для построения развертки поверхности усеченной пирамиды в графической работе №12: Графическая работа 12