Проекции прямой

Зависимость между декартовыми координатами принадлежащих плоскости точек, выраженная аналитически в виде многочлена первой степени:

Преобразуется в уравнение проекции прямой, когда как минимум один из них равен нулю:
Cz=0;
By=0;
Ax=0.
Например для горизонтальной проекции прямой:

То есть, проекции прямой - линия первого порядка.

Построим проекции прямой, которой принадлежат точки А и В. Спроецировав их на плоскости проекций H, V и W, а затем соединив между собой одноименные проекции A`B`, A"B" и A"`B"` получаем проекции прямой.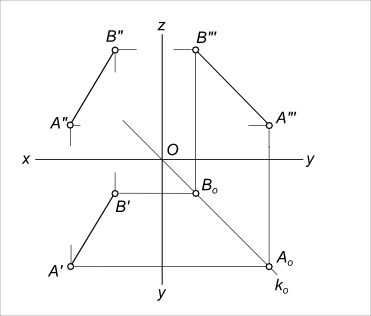

Проекции прямой

При ортогональном проецировании на плоскость прямая проецируется в прямую.
Поэтому для определения проекции прямой достаточно знать проекции двух не тождественных точек, принадлежащих прямой.
Аксиома евклидовой геометрии гласит: «Через две точки проходит единственная прямая».
Отсюда вытекает ответ на вопрос сколько точек определяют положение прямой в пространстве? Ответ две точки.
В связи с этим, построение проекции прямой линии на КЧ сводится к построению проекций двух точек ей принадлежащих.

На эпюре (КЧ) прямая может быть задана проекциями двух точек (отрезком) или непосредственно своими проекциями.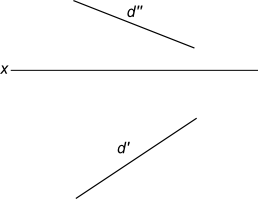

Прямая общего положения

На представленном рисунке положение прямой d определяют проекции прямой d` и d".

Построить проекции прямой зная ее следы lH и lV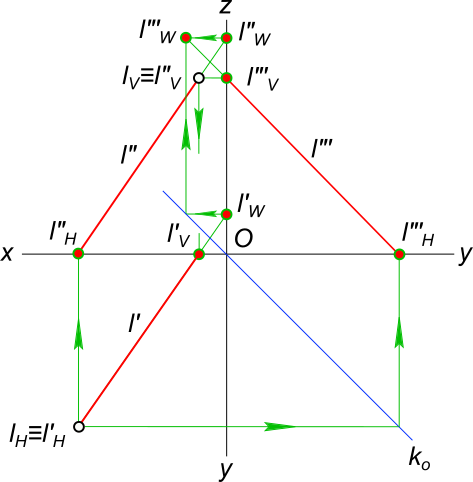

Проекции прямой

Для заданных следов lH и lV находим их проекции l"H и l`V. Соединяя проекции следов l"H и l"V получаем фронтальную проекцию прямой l". Соединяя проекции следов l`H и l`V получаем горизонтальную проекцию прямой l`.