Профильная прямая

Профильная прямая - прямая параллельная профильной плоскости проекции: ω ║ W.

Профильная прямая ω имеет все точки удалеными на одинаковое расстояние от профильной плоскости W:
- горизонтальная проекция любой профильной прямой параллельна оси y: ω` ║ y;
- фронтальная - оси z: ω" ║ z;
- профильная проекция может занимать любое положение.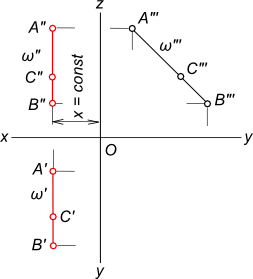

Профильная прямая

Приведенная запись означает: для множества точек C, принадлежащих прямой ω, абсцисса x есть величина постоянная, характеризует удаление точек от профильной плоскости проекций.

Профильная прямая (ω) –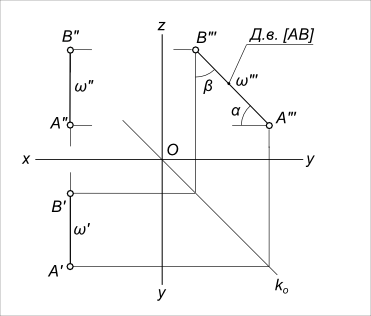

Профильная прямая

имеет следующие признаки и свойства на эпюре (КЧ):
1) горизонтальная проекция профильной прямой ω располагается параллельно оси O_y, фронтальная проекция - располагается параллельно оси O_z;
2) На профильную плоскость проекций без искажения проецируются:
- отрезок, принадлежащий профильной прямой ω: |A"`B"`|=|AB|;
- углы наклона его к плоскостям проекций:
- (α) - к горизонтальной;
- (β) - к фронтальной.

Различают восходящую и нисходящую профильные прямые:
- нисходящая, когда передний конец прямой расположен ниже ее заднего конца (два выше приведенных рисунка);
- восходящая, когда передний конец прямой расположен выше ее заднего конца (ниже приведенный рисунок).
Профильная прямая относится к частному случаю расположения прямой

Кроме общего случая, прямая по отношению к заданной системе плоскостей проекций может занимать частое положение. Прямые частного положения подразделяются на прямые уровня и проецирующие прямые.

Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня.
Существует три вида прямых уровня: горизонталь, фронталь и профильная прямая.

К числу частных случаев расположения прямых можно отнести и прямые, лежащие непосредственно в плоскостях проекций. Их называют прямыми нулевого уровня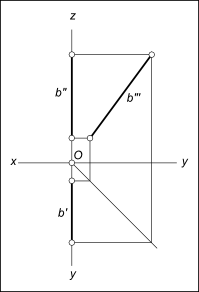

Профильная прямая

На рисунке приведен пример такой прямой: профильная прямая лежит в профильной плоскости проекций, а значит ее фронтальная проекция на эпюре (КЧ) совпадают с осью O_z.

По расположению относительно плоскостей проекций бывают прямые частного положения:
Горизонтальная прямая;
Фронтальная прямая;
Проецирующие прямые.