Горизонтальная прямая

Горизонтальная прямая (горизонталь) - прямая параллельная горизонтальной плоскости проекции: h ║ H.

Горизонтальная прямая имеет все точки удаленными на одинаковое расстояние от плоскости H:
- фронтальная проекция любой горизонтали параллельна оси x: h" ║ x;
- профильная проекция горизонтальной прямой - оси y: h"` ║ y;
- горизонтальная проекция горизонтальной прямой может занимать любое положение.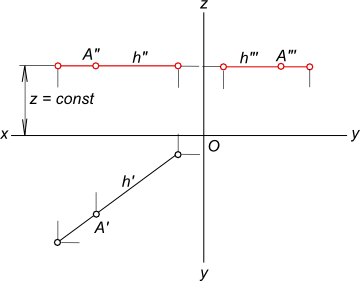

Горизонтальная прямая

Приведенная запись означает: для множества точек A, принадлежащих прямой h, аппликата есть величина постоянная, характеризует удаление точек от горизонтальной плоскости проекций.

Горизонтальная прямая h –

Горизонтальная прямая

имеет следующие признаки и свойства на эпюре (КЧ):
1) Фронтальная проекция горизонтали h" располагается параллельно оси O_х (или в безосном чертеже перпендикулярно линиям связи);
2) На горизонтальную плоскость проекций без искажения проецируются:
- отрезок, принадлежащий горизонтали h: |A`B`|=|AB|;
- углы наклона его к фронтальной (β) и профильной (γ) плоскостям проекций.

Горизонтальная прямая относится к Частному случаю расположения прямой

Кроме общего положения, прямая по отношению к заданной системе плоскостей проекций может занимать частное положение. Прямые частного положения подразделяются на прямые уровня и проецирующие прямые.

Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня. Существует три вида прямых уровня: горизонтальная прямая (горизонталь), фронталь и профильная прямая.

К числу частных случаев расположения прямых можно отнести и прямые, лежащие непосредственно в плоскостях проекций.
Их называют прямыми нулевого уровня.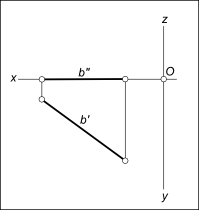

Горизонтальная прямая

На рисунке приведена горизонтальная прямая нулевого уровня: горизонталь h располагается на горизонтальной плоскости проекций, следовательно ее фронтальные проекции находятся на оси O_x.

По расположению относительно плоскостей проекций бывают прямые частного положения:
Фронтальная прямая;
Профильная прямая;
Проецирующие прямые.