Пересекающиеся прямые

Пересекающиеся прямые - это прямые, лежащие в одной плоскости и имеющие одну общую точку, которую называют точкой пересечения прямых.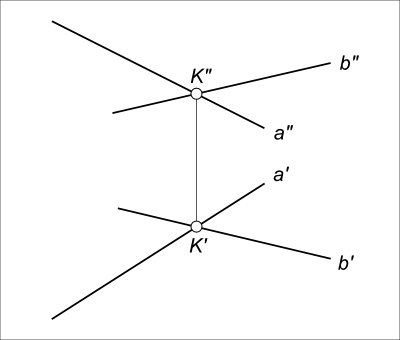

Пересекающиеся прямые

Так как проекция прямой есть прямая, то проекцией пересекающихся прямых будут их пересекающиеся проекции:

Чтобы определить на эпюре (комплексном чертеже), пересекаются ли данные прямые в пространстве, достаточно провести линию связи из одной точки пересечения проекций к другой. Если проекции точки пересечения прямых будут лежать на одной линии связи, то прямые пересекаются.
Чтобы построить на эпюре (комплексном чертеже), пересекающиеся прямые в пространстве, достаточно провести линию связи из одной точки пересечения проекций прямых к другой. Проекцию точки пересечения прямых на другой плоскости проекций находим в пересечении линии проекционной связи, с проекцией одной из пересекающихся прямых, через нее проводим проекцию другой прямой.
Если одна из прямых параллельна профильной плоскости проекций, то для определения положения точки пересечения прямых в пространстве необходимо построить третью (профильную) проекцию.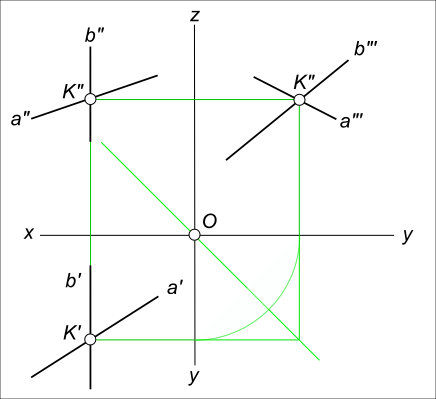

Пересекающиеся прямые

Построить проекции прямой d, пересекающей заданные прямые a, b и c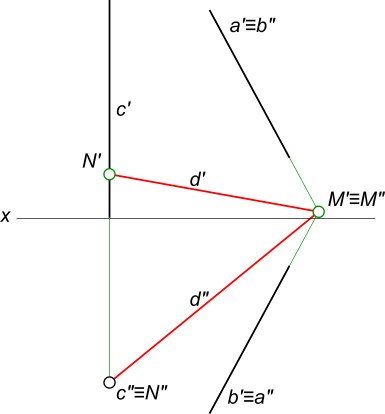

Пересекающиеся прямые

Продолжив проекции прямых a и b находим M` =a` ∩ b` и M"=a" ∩ b" проекции точки M, которые совпадают а поэтому находятся на одной линии проекционной связи и следовательно a и b пересекающиеся прямые. Через точку M пересечения прямых a, b и прямую c проводим прямую d(d`, d"):
M=a ∩ b;
N`= c` ∩ d` ^ N"= c" ∩ d";
N ∈ d ^ M ∈ d