Пересечение прямой с плоскостью

Задача на пересечение прямой с плоскостью - это одна из основных задач, с ее применением сталкиваются при рассмотрении сечения тел плоскостями и пересечения поверхностей.

Нахождение точки встречи прямой с плоскостью, заданной пересекающимися прямыми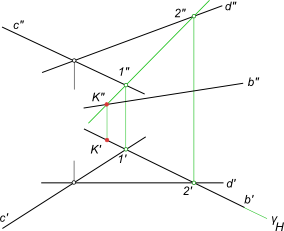

Пересечение прямой с плоскостью

Плоскость и пересекающая ее прямая занимают общее положение.

(γ ∩ α) = l - прямая, пересекающаяся с прямой b.

На пересечение прямой с плоскостью составляем алгоритм нахождения их точки встречи :

1) проводим через b` горизонтальный след γ_H - горизонтально-проецирующей плоскости γ;

2) определяем фронтальную проекцию линии пересечения l, вспомогательной секущей плоскости γ с данной плоскостью α, используя для этого точки 1` и 2` (принадлежащие данной прямой), в которых горизонтальный след γ_H пересекает прямые c` и d`;

3) определяем точку K"=l"∩b". Зная K", находим K` на пересечении b` с линией проекционной связи.

Нахождение точки встречи прямой с плоскостью, заданной параллельными прямыми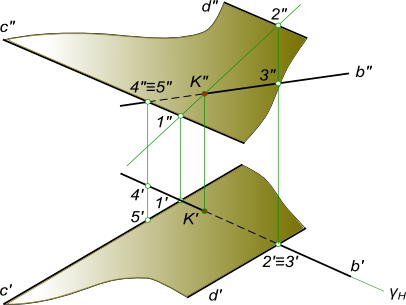

Пересечение прямой с плоскостью

Задача по нахождению точки встречи прямой с плоскостью заданной следами.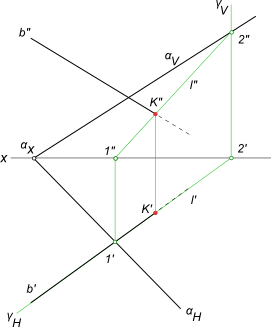

Пересечение прямой с плоскостью

Алгоритм решения не меняется, если плоскость будет задана параллельными прямыми или прямыми, по которым она пересекает плоскости проекций (следы плоскости).

При решении задач на пересечение прямой с плоскостью в качестве вспомогательных плоскостей применяют проецирующие плоскости. Но в случае, например, профильной прямой они бесполезны и тогда надо применить плоскость общего положения.

Найти точку встречи профильной прямой AB с плоскостью α заданной следами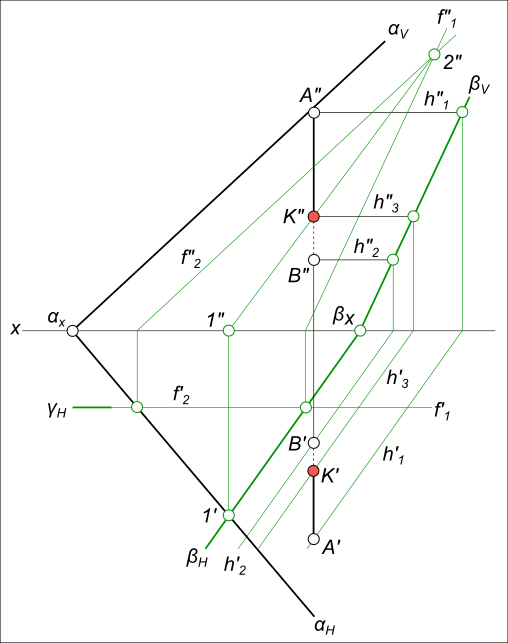

Пересечение прямой с плоскостью

Алгоритм выполнения геометрических построений:
1) Заключаем отрезок AB во вспомогательную секущую плоскость общего положения β;
2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости β с данной плоскостью α;
3) Определяем проекцию K" точки K на пересечении 1"-2" с прямой A"B". Проекция K` точки K может быть найдена: - на пересечении A`B` с 1`-2`; - или как принадлежащая плоскостям α и β.

Найти точку встречи прямой d с плоскостью α(b, c), определить видимость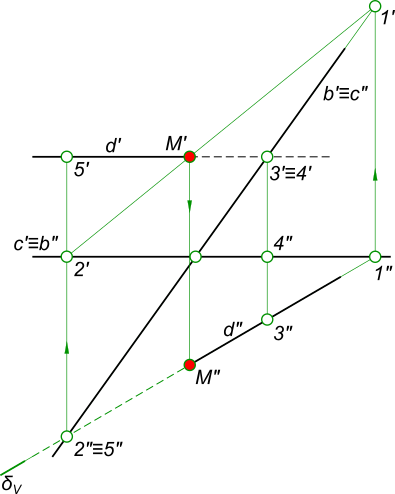

Пересечение прямой с плоскостью

Алгоритм выполнения геометрических построений:
1) Заключаем прямую d во вспомогательную секущую фронтально проецирующую плоскость δ;
2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости δ с данной плоскостью α;
3) Определяем проекцию K` точки K на пересечении 1`-2` с прямой d`. Проекцию K" точки K находим в пересечении d" с линией проекционной связи.

Данный способ решения задачи - найти точку встречи профильной прямой с плоскостью заданной следами применен в статье:
Сечение пирамиды плоскостью

Определение видимости пересечения прямой с плоскостью на плоскостях проекций выполняем, используя Конкурирующие точки 2, 3 и 4, 5.