Сечение прямого кругового конуса

В сечении конической поверхности плоскостью получаются кривые второго порядка - окружность, эллипс, парабола и гипербола. В частом случае при определенном расположении секущей плоскости и когда она проходит через вершину конуса (S∈γ), окружность и эллипс вырождаются в точку или в сечении попадает одна или две образующих конуса.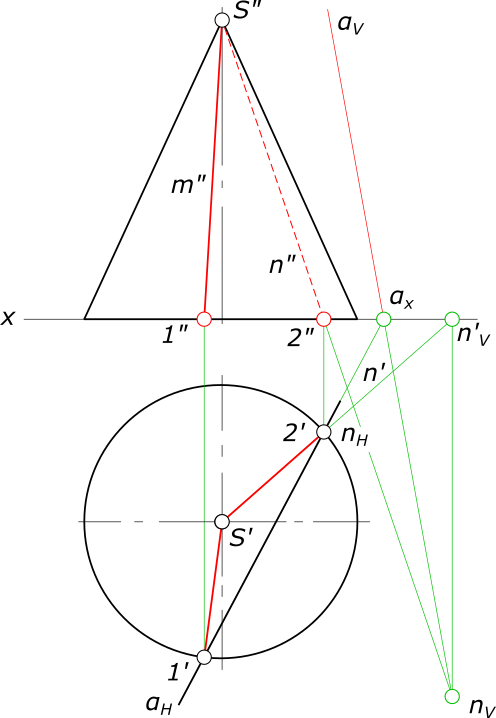

Сечение прямого кругового конуса

Сечение прямого кругового конуса дает - окружность, когда секущая плоскость перпендикулярна к его оси и пересекает все образующие поверхности.

Сечение прямого кругового конуса дает - эллипс, когда секущая плоскость не перпендикулярна к его оси и пересекает все образующие поверхности.

Построим эллиптическое сечение прямого кругового конуса ω плоскостью α, занимающей общее положение.

Решение задачи на сечение прямого кругового конуса плоскостью значительно упрощается, если секущая плоскость занимает проецирующее положение.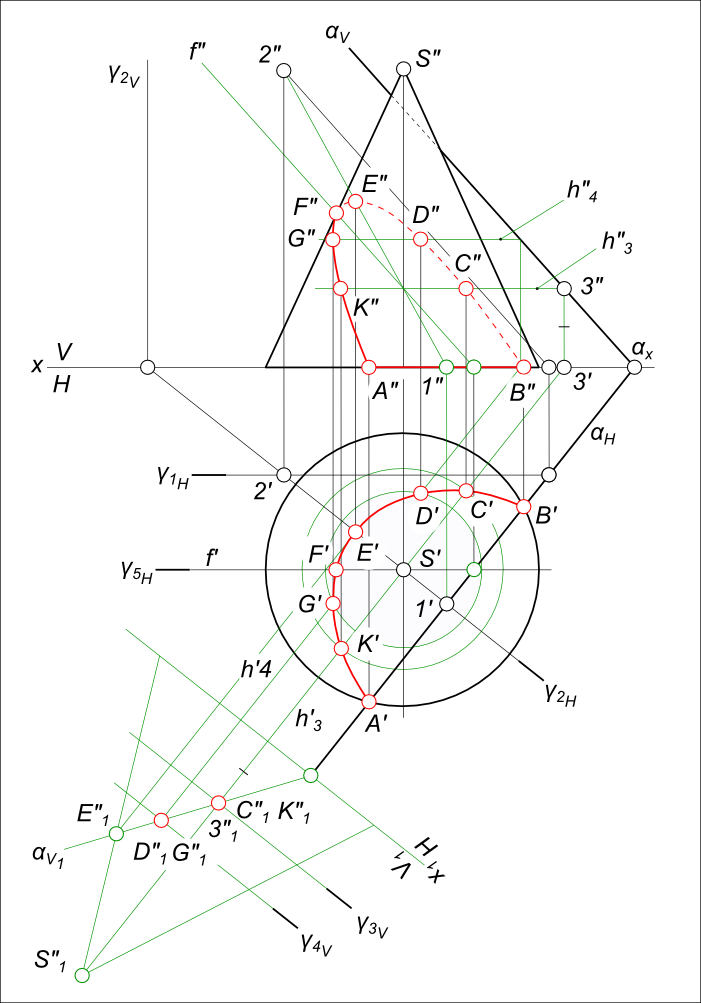

Сечение прямого кругового конуса

Способом перемены плоскостей проекций переведем плоскость α из общего положения в частное - фронтально-проецирующее. На фронтальной плоскости проекций V₁ построим след плоскости α и проекцию поверхности конуса ω. Сечение прямого кругового конуса плоскостью дает эллипс, так как секущая плоскость пересекает все образующие конуса. Эллипс проецируется на плоскости проекций в виде кривой второго порядка.
На следе плоскости α_V берем произвольную точку 3" замеряем ее удаление от плоскости проекций H и откладываем его по линии связи уже на плоскости V₁, получая точку 3"₁. Через нее и пройдет след αV₁. Линия сечения конуса ω - точки A"₁, E"₁ совпадает здесь со следом плоскости. Далее построим вспомогательную секущию плоскость γ3, проведя на фронтальной плоскости проекций V₁ ее след γ_3V1. Вспомогательная плоскость пересекаясь с конической поверхностью ω даст окружность, а пересекаясь с плоскостью α даст горизонтальную прямую h3. В свою очередь прямая пересекаясь с окружностью дает искомые точки C`и K` пересечения плоскости α c конической поверхностью ω. Фронтальные проекции искомых точек C" и K" построим как точки принадлежащие секущей плоскости α.

Для нахождения точки E(E`, E") линии сечения, проводим через вершину конуса горизонтально-проецирующую плоскость γ<sub>2H</sub>, которая пересечет плоскость α по прямой 1-2(1`-2`, 1"-2"). Пересечение 1"-2" с линией связи дает точку E" - наивысшую точку линии сечения.

Для нахождения точки указывающей границы видимости фронтальной проекции линии сечения, проводим через вершину конуса горизонтально-проецирующую плоскость γ_5H и находим горизонтальную проекцию F`искомой точки. Также, плоскость γ<sub>5H</sub> пересечет плоскость α по фронтали f(f`, f"). Пересечение f" с линией связи дает точку F". Соединяем полученные на горизонтальной проекции точки плавной кривой, отметив на ней крайнюю левую точку G - одну из характерных точек линии пересечения.
Затем, строим проекции G на фронтальных плоскостях проекций V1 и V. Все построенные точки линии сечения на фронтальной плоскости проекций V соединяем плавной линией.

Сечение прямого кругового конуса дает - параболу, когда секущая плоскость параллельна одной образующей конуса.

При построении проекций кривых - конических сечений необходимо помнить о теореме: ортогональная проекция плоского сечения конуса вращения на плоскость, перпендикулярную к его оси, есть кривая второго порядка и имеет одним из своих фокусов ортогональную проекцию на эту плоскость вершины конуса.

Рассмотрим построение проекций сечения, когда секущая плоскость α параллельна одной образующей конуса (SD).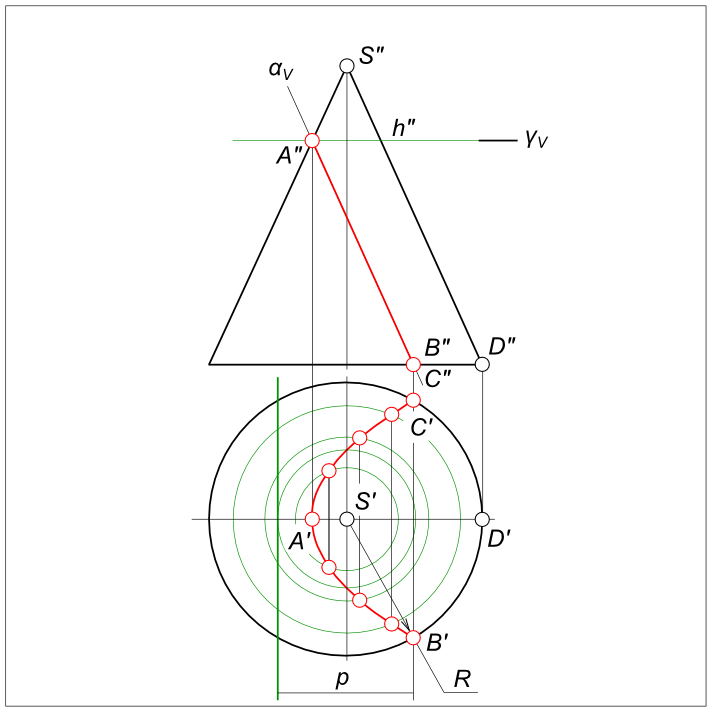

Сечение прямого кругового конуса

В сечении получится парабола с вершиной в точке A(A`, A"). Согласно теореме вершина конуса S проецируется в фокус S`. По известному [S`A`]=R_S` определяем положение директрисы параболы. В последующем точки кривой строятся по уравнению p=R.

Построение проекций сечения, когда секущая плоскость α параллельна одной образующей конуса, может быть выполнено: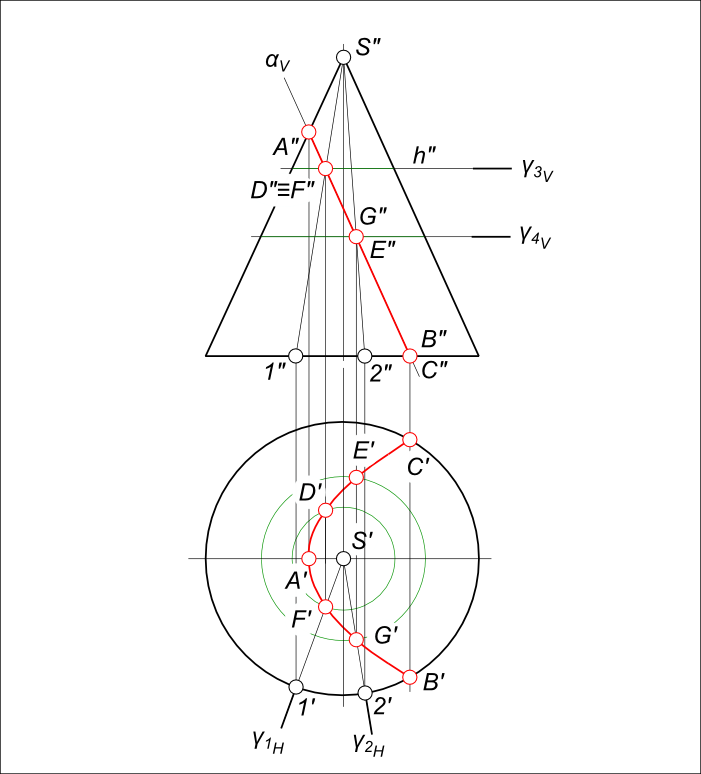

Сечение прямого кругового конуса

- с помощью вспомогательных горизонтально-проецирующих плоскостей проходящих через вершину конуса γ_1H и γ_2H.

Сначала определятся фронтальные проекции точек F", G" - на пересечении образующих S"1", S"2" и следа секущей плоскости α_V. На пересечении линий связи с γ_1H и γ_2H определяться F`, G`.

Аналогично могут быть определены и другие точки линии сечения, например D", E" и D`, E`.

- с помощью вспомогательных фронтально-проецирующих плоскостей ⊥ оси конуса γ_3V и γ_4V.

Проекциями сечения вспомогательных плоскостей и конуса на плоскость H, будут окружности. Линиями пересечения вспомогательных плоскостей с секущей плоскостью α будут фронтально- проецирующие прямые.

Сечение прямого кругового конуса дает - гиперболу, когда секущая плоскость параллельна двум образующим конуса.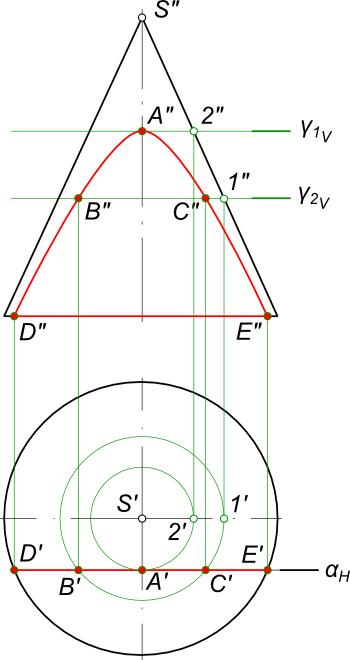

Сечение прямого кругового конуса