Сечение сферы плоскостью

Сечение сферы плоскостью представляет плоскую кривую - окружность, принадлежащую секущей плоскости.
Построить сечение сферы плоскостью общего положения β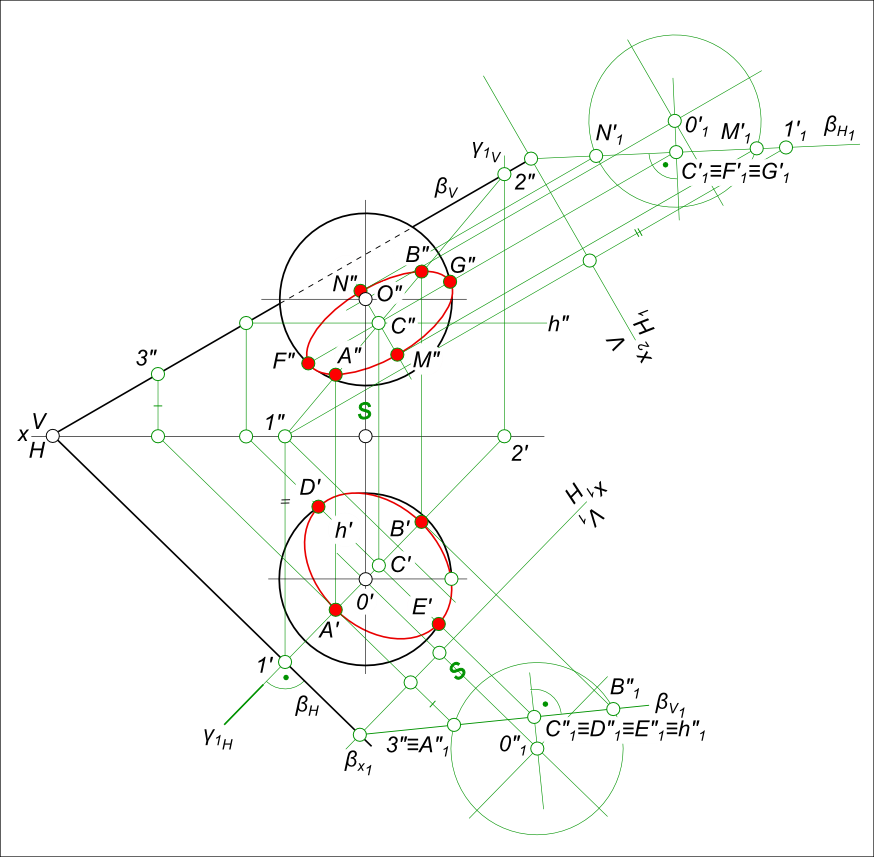

Сечение сферы плоскостью

Так как секущая плоскость общего положения, то эта окружность проецируется на плоскости проекций в виде эллипсов. Для построения эллипса необходимо знать размеры эллипса по его осям большой и малой.
Для тел вращения, к каковым относят цилиндр, конус и сферу, линия сечения может быть построена с характерными точками кривой к которым относятся:
- точки в которых меняется знак видимости;
- точки в которых ее координаты принимают максимальные и минимальные значения:
- x_max; x_min;
- y_max; y_min;
- z_max; z_min;
Использование характерных точек позволяет выполнить более точное построение линии пересечения поверхности вращения и плоскости.

Решение задачи на сечение сферы плоскостью значительно упрощается, если секущая плоскость занимает проецирующее положение.

Способом перемены плоскостей проекций переведем плоскость β из общего положения в частное - фронтально-проецирующее. На фронтальной плоскости проекций V₁ построим след плоскости β и проекцию шара. На следе плоскости β_V берем произвольную точку 3" замеряем ее удаление от плоскости проекций H и откладываем его по линии связи уже на плоскости V₁, получая точку 3"₁. Через нее и пройдет след. Линия сечения шара - точки A"₁, B"₁ совпадает здесь со следом плоскости. Далее на фронтальной плоскости проекций V₁ построим центр окружности сечения - точку C"₁ которую получим восстановив перпендикуляр из центра шара (точка 0"₁) к [A"₁ B"₁] на их пересечении. Далее включаем обратное проецирование: через точки A"₁, B"₁ и C"₁ проводим горизонтали h принадлежащие плоскости β, и на плоскости проекций H через центр шара проводим вспомогательную горизонтально-проецирующую плоскость γ₁. Горизонтальный след плоскости γ₁ пресечет проекцию горизонтали h и определит в этом месте точку C` - центра окружности сечения. Горизонталь h` пересекает проекцию шара в точках D` и E`, определяя тем самым действительную величину отрезка [DE] - большой оси эллипса. Аналогично строятся точки A` и B`, определяющие величину отрезка [A`B`] - малой оси эллипса.

Проекции большой и малой оси эллипса на горизонтальную плоскость проекции H найдены, а это означает что эллипс - проекция окружности сечения на H может быть построен, смотри статью: Окружность

Повторим те же действия на для фронтальной плоскости проекций V и построим другой эллипс - проекцию окружности сечения на V.

Для нахождения точек указывающих границы видимости горизонтальной проекции окружности сечения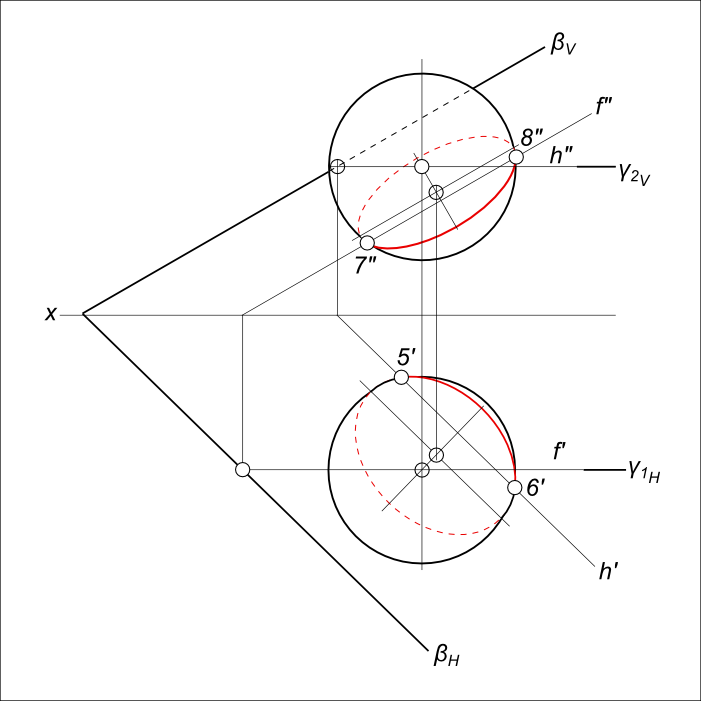

Сечение сферы плоскостью

проводим через центр шара фронтально-проецирующую плоскость γ₂ ⊥ V, которая пересечет плоскость β по горизонтали h(h`, h"). Линия h` пересекается с горизонтальной проекцией окружности сечения по точкам 5,6 указывающим границу видимости. Точки окружности сечения расположенные на фронтальной проекции ниже следа плоскости γ₂, на горизонтальной плоскости проекции H будут располагаться слева от отрезка [5`, 6`] - и будут на ней невидимы.

Для нахождения точек указывающих границы видимости фронтальной проекции окружности сечения. Проводим через центр шара горизонтально-проецирующую плоскость γ₁ ⊥ H, которая пересечет плоскость β по фронтали f(f`, f"). Линия f" пересекается с фронтальной проекцией окружности сечения по точкам 7", 8" указывающим границу видимости. Точки окружности сечения расположенные на горизонтальной проекции выше следа плоскости γ₁, на фронтальной плоскости проекции V будут располагаться слева от отрезка [7", 8"] - и будут на ней невидимы.