Сечение тора плоскостью

Сечение тора плоскостью представляет плоскую кривую, принадлежащую секущей плоскости.
Поверхность тора - геометрическое место точек удаленных на одинаковое расстояние от его оси, представляющей собой окружность.
Из чего следует, что линия сечения тора плоскостью - геометрическое место точек плоскости удаленных на одинаковое расстояние от его оси, представляющей собой окружность.
Построить сечение тора плоскостью общего положения β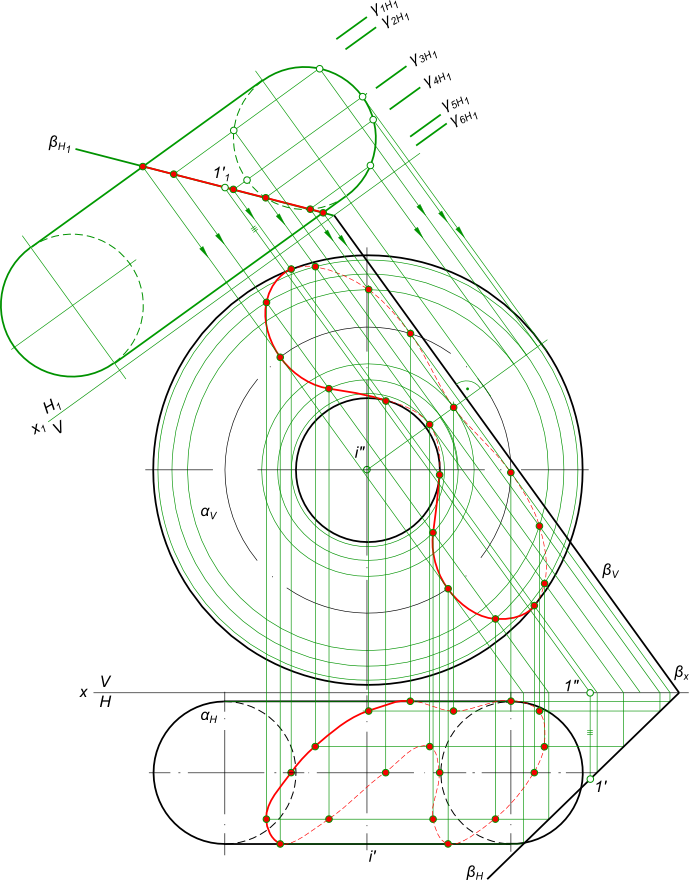

Сечение тора плоскостью

Так как секущая плоскость общего положения, то эта плоская кривая проецируется на плоскости проекций также в виде плоской кривой.
Для тел вращения, к каковым относят тор, цилиндр, конус и сферу, линия сечения может быть построена с использованием характерных точек кривой к которым относятся:
- точки в которых меняется знак видимости;
- точки в которых ее координаты принимают максимальные и минимальные значения:
- x_max; x_min;
- y_max; y_min;
- z_max; z_min;
Использование характерных точек позволяет выполнить более точное построение линии пересечения поверхности вращения и плоскости.

Решение задачи на сечение тора плоскостью значительно упрощается, если секущая плоскость занимает проецирующее положение.

Способом перемены плоскостей проекций переведем плоскость β из общего положения в частное - горизонтально проецирующее.
На горизонтальной плоскости проекций H₁ построим след плоскости β и проекцию тора. Для этого на следе плоскости β_H берем произвольную точку 1` замеряем ее удаление от плоскости проекций V и откладываем его по линии связи уже на плоскости H<sub>1</sub>, получая точку 1`₁. Через нее и пройдет след β_H1.
Линия сечения тора совпадает со следом плоскости β_H1.
Через характерные точки кривой проводим вспомогательные секущие плоскости γ1_H1, γ2_H1, ..., γ6_H1, в пересечении которых с тором получим окружности, а в пересечении с плоскостью α - ее горизонтали h1₁, h2₁, ..., h6₁.
Далее включаем обратное проецирование:
- через характерные точки проводим линии связи (на плоскости проекций V они совпадают с фронталями) и в их пересечении с проекциями окружностей на плоскости проекций V получим искомые точки линии сечения; - на горизонтальный плоскости H искомые точки линии сечения строим как принадлежащие секущей плоскости: в пресечении их линий связи с фронталями f1, f2 ..., f6.

Нахождения точек указывающих границы видимости горизонтальной и фронтальной проекции линии сечения поступаем аналогично тому как изложено в статье:
Сечение сферы плоскостью