Сечение цилиндра плоскостью

Сечение цилиндра плоскостью,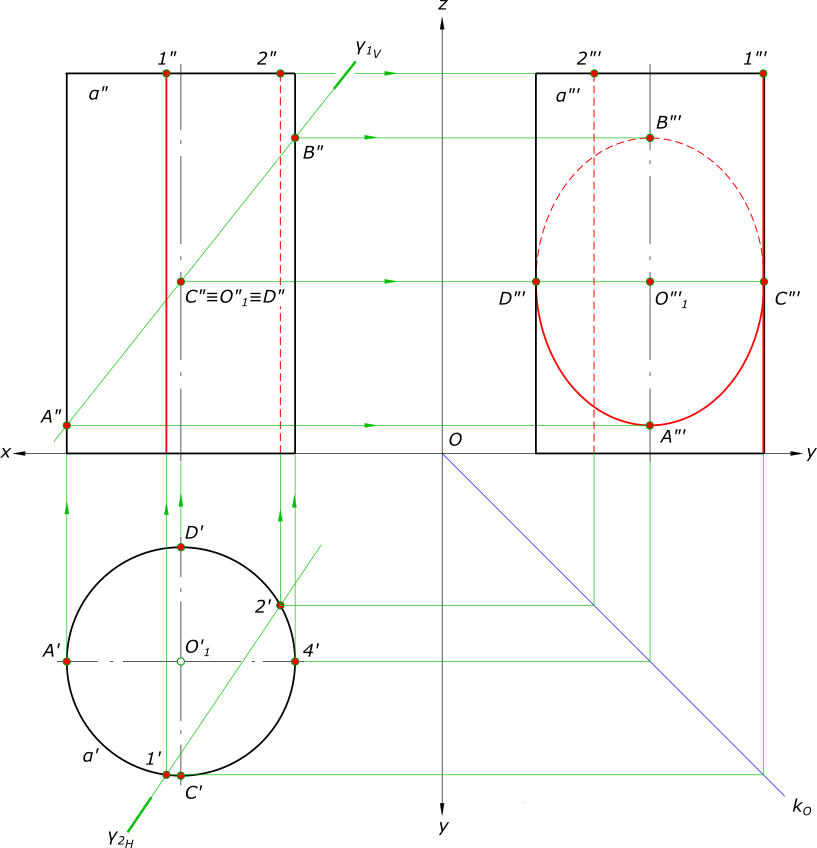

Сечение цилиндра плоскостью

если пересекаются все образующие (Y1), представляет плоскую кривую второго порядка - окружность или эллипс, принадлежащую секущей плоскости. В частом случае, при определенном расположении секущей плоскости (Y2), когда она проходит через две образующие, сечение цилиндра представляет собой прямоугольник

Сечение прямого кругового цилиндра дает - окружность, когда секущая плоскость перпендикулярна к его оси и пересекает все образующие поверхности.

Построение третьей проекции линии сечения цилиндра плоскостью по двум заданным представлено на рисунке. Здесь сечение прямого кругового цилиндра - эллипс с большой осью AB и малой осью CD, когда секущая плоскость не перпендикулярна к его оси и пересекает все образующие поверхности.

Построим эллиптическое сечение прямого кругового цилиндра ω плоскостью α, занимающей общее положение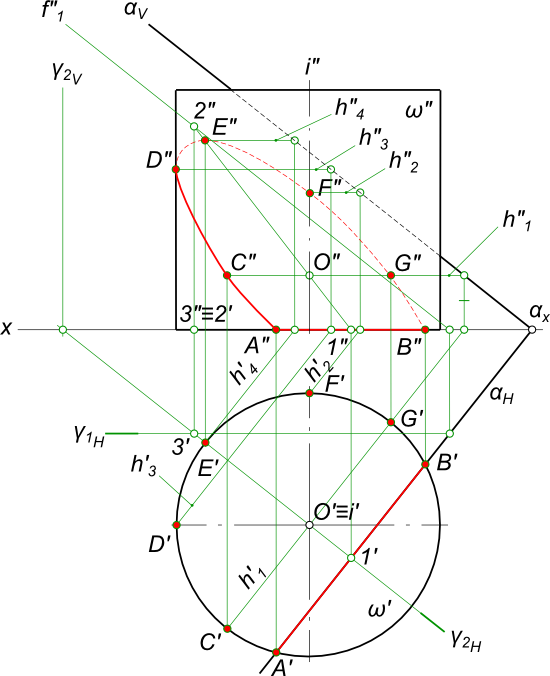

Сечение цилиндра плоскостью

Решение задачи на сечение прямого кругового цилиндра плоскостью, в данном случае значительно упрощается потому, образующие цилиндра занимают проецирующее положение:
- проекции точек A и B линии пересечения находим без каких-либо дополнительных построений в пересечении окружности основания цилиндра и горизонтального следа αΗ секущей плоскости;
- горизонтальные проекции остальных точек линии пересечения находятся на окружности основания цилиндра левее горизонтального следа αΗ.
Задавая горизонтальные проекции ряда точек, в том числе и характерных точек кривой линии пересечения - точки D это граница видимости и E это наивысшая, находим их недостающие фронтальные проекции из условия принадлежности плоскости α:
- проводим через точки горизонтали плоскости h1, h2, h3 и h4 и в пересечении их с линиями связи точек находим фронтальные проекции C", D", E", F" и G".
- проекции A", B", C", D", E", F" и G" соединяем плавной кривой линией и получаем недостающую фронтальную проекцию линии пересечения.

Определение видимости линии пересечения и цилиндра на плоскости проекций выполняем с использованием конкурирующих точек.